Research
My research interests are coding theory with applications to communication and distributed systems and quantum error-correcting codes.
Codes For Distributed Storage
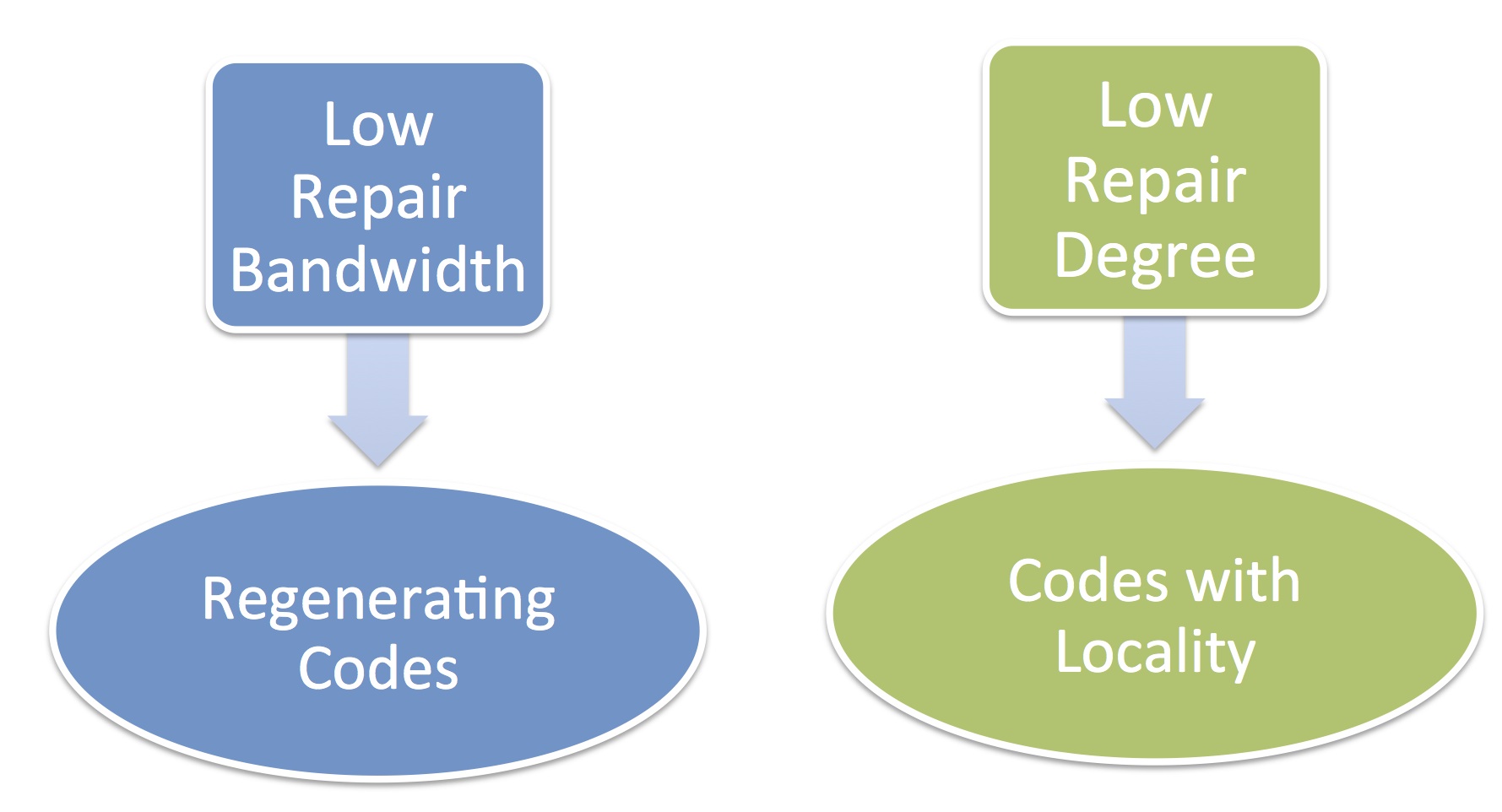
In a distributed storage system, node failures are modelled as erasures and codes are employed to provide reliability against failures. Reliability of a DSS gives guarantee against worst case node failures. However, single node failures are the the most common case of node failures. Though maximal distance separable (MDS) codes offer very good reliability for a given storage overhead, they suffer from the disadvantage that the number of nodes contacted for node repair in case of single node failure is large. To enable more efficient node repair in case of single node failures, regenerating codes and codes with locality (also known as locally repairable codes (LRC)) have been proposed in literature. While regenerating codes tradeoff storage overhead for repair bandwidth (amount of data downloaded for node repair) , codes with locality tradeoff storage overhead for the number of nodes contacted for repair.
Codes with Locality
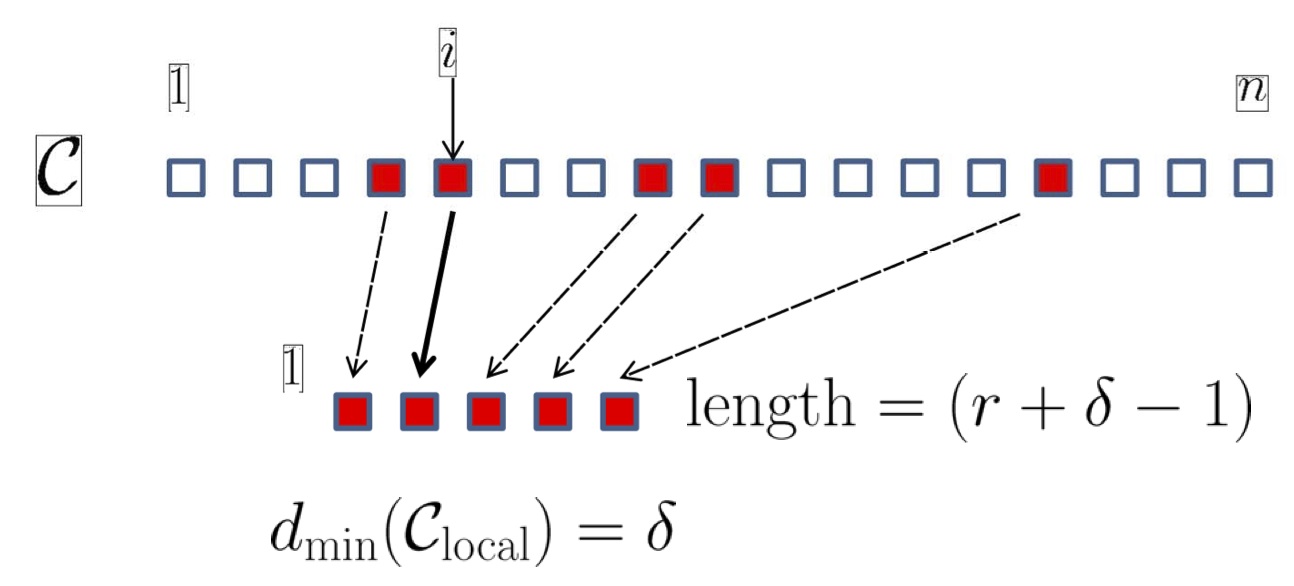
The notion of codes with locality has been originally introduced to handle single node failures. We have come up with several notions of locality to handle multiple node failures. In one line of work, we have combined the ideas of regenerating codes and codes with locality to design a new class of codes called codes with local regeneration. In a second line of work, sequential repair of node failures is allowed, when two nodes fail and codes with sequential locality have been studied.
Cooperative Regenerating Codes
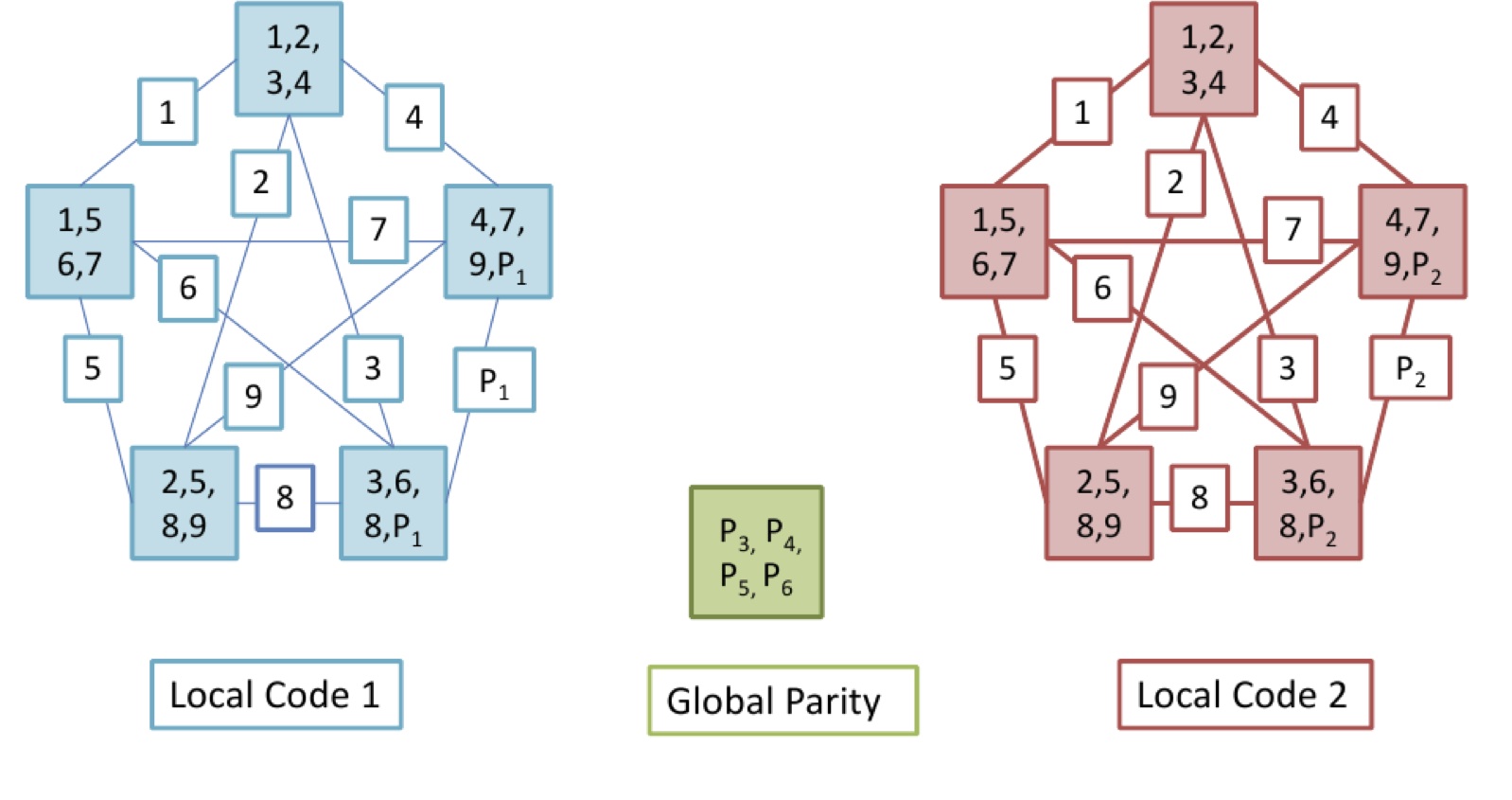
Regenerating codes minimize the repair bandwidth to repair a failed node and hence enable efficient repair. Cooperative regenerating codes achieve a similar objective in the case of multiple node failures. We designed near optimal cooperative regenerating codes with low subpacketization. In another work, we consider the setup where the nodes in the network are placed in racks. In case of node failures, the intra-rack repair has no cost associated with it and only inter-rack repair bandwidth is considered.
Maximally Recoverable Codes
Maximally recoverable codes are a class of codes which recover from all potentially recoverable erasure patterns given the locality constraints of the code. In earlier works, these codes have been studied in the context of codes with locality. Based on connection to matroids, we derived the weight distribution of maximally recoverable codes. We also considered the locality constraints imposed by codes with two-level hierarchical locality and define maximally recoverable codes with data-local and local hierarchical locality. This work has been published in Proceedings of National Conference of Communications 2019 and also won the Best Paper Award (Runner Up) in the conference.
Codes for Distributed Computing
Distributed computing uses multiple distributed servers to process the job. A job in distributed computing consists of multiple parallel tasks, which can be computed on different servers, and the job is finished when all the tasks are complete. The slowest tasks that determine the job execution time are called stragglers. Coding theoretic techniques have been proposed to achieve high-quality algorithmic results in the face of uncertainty, including mitigation of stragglers. The different distributed computing applications include matrix-vector multiplication, matrix-matrix multiplication, computation of gradients, polynomial evaluations and so on. We are interested in the distributed gradient computation problem in the presence of stragglers.
Tiered Gradient Codes
We considered a framework which is a variant of the gradient coding setting in which we exploit the flexibility where all tasks are not started at the service request time. This reduces the overall task size at each server and thus the task completion time, as well as the overall server utilization cost. We proposed gradient codes which allow for delayed launch of tasks in two phases.
Gradient Coding with Partial Recovery
Approximate gradient coding has also been considered in earlier works where the L2-norm between the computed gradient vector and the actual gradient vector is minimized. We considered the problem of approximate gradient coding which allowed for sum of fraction of partial gradients to be recovered at the master. We derived a lower bound on the computation load of any scheme and also proposed two strategies which achieve this lower bound, albeit at the cost of high communication load. We also proposed schemes based on cyclic assignment which utilize smaller number of data partitions and have a lower communication load.
Hybrid Coded MapReduce
Though this topic falls under the broad area of distributed computing, it’s different from the straggler mitigation which we were discussing till now. Coded MapReduce has been proposed to reduce the communication cost during data shuffling by creating coding opportunities. In contrast to homogenous architecture assumed in Coded MapReduce system model, distributed computing systems typically have server-rack architecture. The servers within a rack are connected via a Top of Rack switch and servers across racks are connected via a Root switch which connects several Top of Rack switches. It is also well known that cross-rack traffic is bottlenecked by the Root switch and hence higher amount of cross-rack traffic can result in lower job completion times. We proposed a Hybrid Coded MapReduce scheme which offered a low cross-rack traffic at the cost of increased intra-rack traffic.
Index Coding and Coded Data Rebalancing
In the index coding problem, a source sends messages over a broadcast to a bunch of receivers, each receiver has a set of demanded messages and also a set of side information messages. By applying coded broadcasting, it has been shown that the number of transmissions over the broadcast channel can be minimized, while meeting the demands of all the receivers. Index coding has applications in satellite communication, content broadcasting and interference management.
Rate 1/3 Index Coding
Linear index coding can be formulated as an interference alignment problem, in which precoding vectors of the minimum possible length are to be assigned to the messages in such a way that the precoding vector of a demand (at some receiver) is independent of the space of the interference (non side-information) precoding vectors. An index code has rate 1/3 if the assigned vectors are of length 3. We derived necessary and sufficient conditions for an index coding problem to be of rate 1/3.
Locally Decodable Index Codes
An index code for broadcast channel with receiver side information is locally decodable if each receiver can decode its demand by observing only a subset of the transmitted codeword symbols instead of the entire codeword. Conventional index coding solutions assume that the receivers observe the entire codeword, and as a result, for these codes the number of codeword symbols queried by a user per decoded message symbol, which we refer to as locality, could be large. We posed the locally decodable index coding problem as that of minimizing the broadcast rate for a given value of locality (or vice versa). For this problem, we identified the optimal broadcast rate corresponding to the minimum possible value of locality for all single unicast problems and designed codes that achieve the optimal trade-off between locality and rate.
Coded Data Rebalancing
Distributed databases often suffer unequal distribution of data among storage nodes, which is known as data skew, which arises from a number of causes such as removal of existing storage nodes and addition of new empty nodes to the database. Data skew leads to performance degradations and thus necessitates ‘rebalancing’ at regular intervals to reduce the amount of skew. We defined an r-balanced distributed database as a distributed database in which the storage across the nodes has uniform size, and each bit of the data is replicated in r distinct storage nodes. We designed such balanced databases along with associated rebalancing schemes which maintain the r-balanced property under node removal and addition operations.
Codes and RL for Blockchains
A blockchain consists of a chain of blocks where each block contains a set of transactions. It is an append-only ledger where blocks are appended to the blockchain one at a time, starting from the genesis block where each block addition requires the nodes to finding a solution to a cryptographic puzzle (also known as POW - proof of work). Such nodes are called miners. With the rapidly growing ledger size of the blockchain, full nodes have to incur a high cost in terms of storage. As of May’20, the size of Bitcoin blockchain is approximately 350.54 GB, and for Ethereum it has grown to 393.99GB. Erasure codes are helpful in reducing the storage costs of the full nodes.
Secure Regenerating Codes for Low Bootstrap Costs in Sharded Blockchains
In literature, sharding has been proposed to scale blockchains so that storage and transaction efficiency of the blockchain improves at the cost of security guarantee. In the context of sharding, we came up with a new protocol termed as Secure-Repair-Blockchain (SRB), which aims to decrease the storage cost at the miners. In addition, SRB also decreases the bootstrapping cost, which allows for new miners to easily join a sharded blockchain. In order to decrease the amount of data that is transferred to the new node joining a shard, the concept of exact repair secure regenerating codes is used. This work was funded by Qualcomm Innovation Fellowship.
Secure Raptor Encoder and Decoder
In a blockchain network, full nodes aid in decentralization by validating incoming transactions and also by assisting new nodes who want to join the network. However, due to the high storage cost incurred by full nodes, the total number of full nodes in a system is falling. In order to curb this problem and maintain decentralization, a secure fountain code (SeF) approach has been proposed earlier, where a class of fountain codes known as LT codes have been used. In this work, we designed Secure Raptor encoder and decoder, which in addition to reducing storage costs, also has constant decoding time.
Reinforcement Learning for Prism
Prism is a recent blockchain algorithm that achieves the physical limit on throughput and latency without compromising security. We proposed a Deep Reinforcement Learning-based Prism Blockchain (DRLPB) scheme which dynamically optimizes the parameters of Prism blockchain and helps in achieving a better performance. In DRLPB, we applied two widely used DRL algorithms, Dueling Deep Q Networks (DDQN) and Proximal Policy Optimization (PPO).
Polar Codes and Reed Muller Codes
In 2009, Erdal Arikan invented these class of codes. These codes achieve channel capacity for binary symmetric discrete memoryless channels. The encoding and decoding complexity of polar codes is O(N log N) where N is the block length of the code. The encoder is based on a transform known as polarizing transform, which is obtained by taking tensor product of a certain 2 × 2 matrix log N times. A sub-optimal decoder, known as successive cancellation decoder, has been employed by Arikan to prove that polar codes achieve capacity (sub-optimal since it's not maximum a-posteriori decoder). Though these codes achieve capacity, the probability of error goes to zero very slowly as function of block length, O(2^−√N). Hence, the practical applicability of these capacity-achieving codes was initially doubtful, since Turbo and LDPC codes gave very good performance in practical settings. To improve the finite block-length error performance, an improved decoder known as successive cancellation list decoder (with manageable decoding complexity) has been proposed. It has been shown that list size of L = 32 with Cyclic Redundancy Check (CRC) gives error performance comparable to those of Turbo codes and LDPC codes for medium block lengths. After these developments, Polar codes gained a lot of attention even in industry. It has been decided in the 3GPP meetings that Polar codes will be employed for the control channel of 5G NR (New Radio). Reed Muller codes are close relatives of polar codes and are channel independent.
Consultancy project on Development of Polar Encoder and Decoder for 5G New Radio
We have implemented polar encoder and decoder according to specifications given in 5G New Radio standard. We have developed fixed point code as well, which can be later converted to RTL.
Polarization of Product Kernels
The original kernel proposed by Arikan was a 2 × 2 matrix. Though it achieves capacity asymptotically, the finite length performance of this kernel is not comparable to that of random codes. It has been observed that larger kernels give better finite length performance. A natural way to construct larger kernels from smaller kernels is by taking Kronecker products. We consider the polar codes obtained using product kernels and characterize their properties in relation to the properties of the component kernels.
Combinatorial List Decoding
List decoding generalizes the concept of unique decoding of codes and allows for larger decoding radius or equivalently more number of errors. In recent literature, the problem of combinatorial list decoding has been considered and a generalized Singleton bound has been derived which relates the blocklength, list size, decoding radius and the field size. This allows for a decoding radius beyond the Johnson radius which was earlier known for list decoding. It has also been shown that higher order generalizations of MDS codes are optimal with respect to the generalized Singleton bound.
Structure of Higher-Order MDS Codes
In the context of higher-order MDS codes, we studied the necessary and sufficient conditions for a code to be a higher order MDS code. We also established that puncturing and psuedo-shortening kind of operations preserve the higher order MDS property of Reed-Solomon Codes. Also, we have derived new field-size upper bounds on these codes. This work was funded by Qualcomm Innovation Fellowship.
Channel Codes and Decoders based on Deep Learning
Conventionally, channel coding has been shown to achieve capacity for long block lengths. Examples of codes include Turbo and LDPC codes. With the requirements of low latency communications, it is necessary to design good codes of very short block length. In the short block length regime, the natural choice of codes is convolutional codes, since they have low encoding and decoding complexity. Recently, there has been work where deep learning has been applied to perform the decoding of existing codes like convolutional codes and Turbo codes. In addition, learning has also been used to design encoder-decoder pairs which perform better than convolution codes in the short block length regime.
Data-Driven Decoder for Trellis Coded Modulation
Trellis coded modulation (TCM) is a technique combining modulation with coding using trellises designed with heuristic techniques that maximize the minimum Euclidean distance of a codebook. We propose a neural networks based decoder for decoding TCM. We showed that a CNN layer following a recurrent neural network gave better decoding performance and provide justification for the same. We also show the generalization capability of the decoder and also its robustness to noise modelling.