The power and speed of modern digital computers is truly astounding. No human can ever hope to compute a million operations a second. However, there are some tasks for which even the most powerful computers cannot compete with the human brain, perhaps not even with the intelligence of an earthworm.
Imagine the power of the machine which has the abilities of both computers and humans. It would be the most remarkable thing ever. And all humans can live happily ever after (or will they?). This is the aim of artificial intelligence in general.
Neural Networks approaches this problem by trying to mimic the structure and function of our nervous system. Many researchers believe that AI (Artificial Intelligence) and neural networks are completely opposite in their approach. Conventional AI is based on the symbol system hypothesis. Loosely speaking, a symbol system consists of indivisible entities called symbols, which can form more complex entities, by simple rules. The hypothesis then states that such a system is capable of and is necessary for intelligence.
The general belief is that Neural Networks is a sub-symbolic science. Before symbols themselves are recognized, some thing must be done so that conventional AI can then manipulate those symbols. To make this point clear, consider symbols such as cow, grass, house etc. Once these symbols and the "simple rules" which govern them are known, conventional AI can perform miracles. But to discover that something is a cow is not trivial. It can perhaps be done using conventional AI and symbols such as - white, legs, etc. But it would be tedious and certainly, when you see a cow, you instantly recognize it to be so, without counting its legs.
But this belief - that AI and Neural Networks are completely opposite, is not valid because, even when you recognize a cow, it is because of certain properties which you observe, that you conclude that it is a cow. This happens instantly because various parts of the brain function in parallel. All the properties which you observe are "summed up". Certainly there are symbols here and rules - "summing up". The only difference is that in AI, symbols are strictly indivisible, whereas here, the symbols (properties) may occur with varying degrees or intensities.
Progress in this area can be made only by breaking this line of distinction between AI and Neural Networks, and combining the results obtained in both, towards a unified framework.
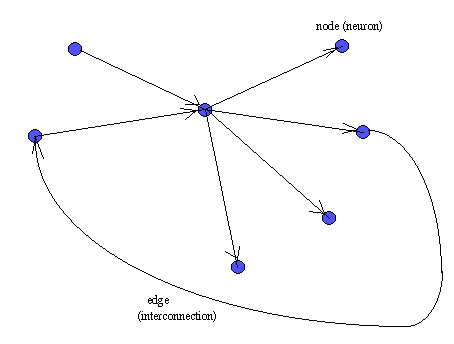
For our purpose, it will be sufficient to know that the nervous system consists of neurons which are connected to each other in a rather complex way. Each neuron can be thought of as a node and the interconnections between them are edges.

Such a structure is called as a directed graph. Further, each edge has a weight associated with it which represents how much the two neurons which are connected by it can interact. If the weight is more, then the two neurons can interact much more - a stronger signal can pass through the edge.
The nature of interconnections between 2 neurons can be such that - one neuron can either stimulate or inhibit the other. An interaction can take place only if there is an edge between 2 neurons. If neuron A is connected to neuron B as below with a weight w,
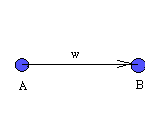
then if A is stimulated sufficiently, it sends a signal to B. The signal depends on the weight w, and the nature of the signal, whether it is stimulating or inhibiting. This depends on whether w is positive or negative. If sufficiently strong signals are sent, B may become stimulated.
Note that A will send a signal only if it is stimulated sufficiently, that is, if its stimulation is more than its threshold. Also if it sends a signal, it will send it to all nodes to which it is connected. The threshold for different neurons may be different. If many neurons send signals to A, the combined stimulus may be more than the threshold.
Next if B is stimulated sufficiently, it may trigger a signal to all neurons to which it is connected.
Depending on the complexity of the structure, the overall functioning may be very complex but the functioning of individual neurons is as simple as this. Because of this we may dare to try to simulate this using software or even special purpose hardware.
We have seen that the functioning of individual neurons is quite simple. Then why is it difficult to achieve our goal of combining the abilities of computers and humans ?
The difficulty arises because of the following -
Given some input, if the neural network makes an error, then it can be determined exactly which neurons were active before the error. Then we can change the weights and thresholds appropriately to reduce this error.
For this approach to work, the neural network must "know" that it has made a mistake. In real life, the mistake usually becomes obvious only after a long time. This situation is more difficult to handle since we may not know which input led to the error.
Also notice that this problem can be considered as a generalization of the previous problem of determining the neural network structure. If this is solved, that is also solved. This is because if the weight between two neurons is zero then, it is as good as the two neurons not being connected at all. So if we can figure out the weights properly, then the structure becomes known. But there may be better methods of determining the structure.
It is usually assumed that such details will not affect the functioning of the simulated neural netwok much. But may be it will.
Another example of deviation from normal functioning is that some edges can transmit signals in both directions. Actually, all edges can transmit in both directions, but usually they transmit in only 1 direction, from one neuron to another.
To cope with the difficulties mentioned in the previous section, the problem has been divided into subproblems. Different types of neural networks have been proposed. Each type restricts the kind of connections that are possible. For example it may specify that if one neuron is connected to another, then the 2nd neuron cannot have another connection towards the first. The type of connections possible is generally referred to as the architecture of the the neural network.
Whenever the neural network makes a mistake, some weights and thresholds have to be changed to compensate for this error. The rules which govern how exactly these changes are to take place, is called as the learning algorithm. Different types of neural networks may have different learning algorithms.
The term `architecture' has been much abused in the history of mankind. It has many meanings depending on whether you are talking about buildings, inside of computers or neural networks among other things. Even in neural networks, the term architecture and what we have been referring to as `type' of neural network are used interchangeably. So when we refer to such and such an architecture, it means the set of possible interconnections (also called as topology of the network) and the learning algorithm defined for it.
Each type of neural network has been designed to tackle a certain class of problems. Hopefully, at some stage we will be able to combine all the types of neural networks into a uniform framework. Hopefully, then we will reach our goal of combining brains and computers.
We shall now try to understand different types of neural networks.
This is a very simple model and consists of a single `trainable' neuron. Trainable means that its threshold and input weights are modifiable. Inputs are presented to the neuron and each input has a desired output (determined by us). If the neuron doesn't give the desired output, then it has made a mistake. To rectify this, its threshold and/or input weights must be changed. How this change is to be calculated is determined by the learning algorithm.
The output of the perceptron is constrained to boolean values - (true,false), (1,0), (1,-1) or whatever. This is not a limitation because if the output of the perceptron were to be the input for something else, then the output edge could be made to have a weight. Then the output would be dependant on this weight.
The perceptron looks like -
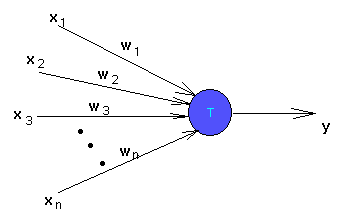
The output y is 1 if the net input which is
w1 x1 + w2 x2 + ... + wn xn
is greater than the threshold T. Otherwise the output is zero.
The idea is that we should be able to train this perceptron to respond to certain inputs with certain desired outputs. After the training period, it should be able to give reasonable outputs for any kind of input. If it wasn't trained for that input, then it should try to find the best possible output depending on how it was trained.
So during the training period we will present the perceptron with inputs one at a time and see what output it gives. If the output is wrong, we will tell it that it has made a mistake. It should then change its weights and/or threshold properly to avoid making the same mistake later.
Note that the model of the perceptron normally given is slightly different from the one pictured here. Usually, the inputs are not directly fed to the trainable neuron but are modified by some "preprocessing units". These units could be arbitrarily complex, meaning that they could modify the inputs in any way. These units have been deliberately eliminated from our picture, because it would be helpful to know what can be achieved by just a single trainable neuron, without all its "powerful friends".
To understand the kinds of things that can be done using a perceptron, we shall see a rather simple example of its use - Compute the logical operations "and", "or", "not" of some given boolean variables.
Computing "and": There are n inputs, each either a 0 or 1. To compute the logical "and" of these n inputs, the output should be 1 if and only if all the inputs are 1. This can easily be achieved by setting the threshold of the perceptron to n. The weights of all edges are 1. The net input can be n only if all the inputs are active.
Computing "or": It is also simple to see that if the threshold is set to 1, then the output will be 1 if atleast one input is active. The perceptron in this case acts as the logical "or".
Computing "not": The logical "not" is a little tricky, but can be done. In this case, there is only one boolean input. Let the weight of the edge be -1, so that the input which is either 0 or 1 becomes 0 or -1. Set the threshold to 0. If the input is 0, the threshold is reached and the output is 1. If the input is -1, the threshold is not reached and the output is 0.
There are problems which cannot be solved by any perceptron. Infact there are more such problems than problems which can be solved using perceptrons. The most often quoted example is the XOR problem - build a perceptron which takes 2 boolean inputs and outputs the XOR of them. What we want is a perceptron which will output 1 if the two inputs are different and 0 otherwise.
Input | Desired Output --------|---------------- 0 0 | 0 0 1 | 1 1 0 | 1 1 1 | 0Consider the following perceptron as an attempt to solve the problem -
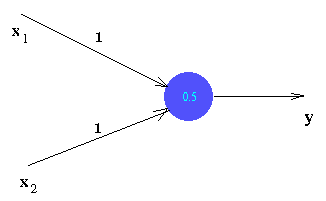
If the inputs are both 0, then net input is 0 which is less than the threshold (0.5). So the output is 0 - desired output.
If one of the inputs is 0 and the other is 1, then the net input is 1. This is above threshold, and so the output 1 is obtained.
But the given perceptron fails for the last case. To see that no perceptron can be built to solve the problem, try to build one yourself.
The inputs that we have been referring to, of the form (x1, x2, ..., xn) are also called as patterns. If a perceptron gives the correct, desired output for some pattern, then we say that the perceptron recognizes that pattern. We also say that the perceptron correctly classifies that pattern.
Since a pattern by our definition is just a sequence of numbers, it could represent anything -- a picture, a song, a poem... anything that you can have in a computer file. We could then have a perceptron which could learn such inputs and classify them eg. a neat picture or a scribbling, a good or a bad song, etc. All we have to do is to present the perceptron with some examples -- give it some songs and tell it whether each one is good or bad. (It could then go all over the internet, searching for songs which you may like.) Sounds incredible? Atleast thats the way it is supposed to work. But it may not. The problem is that the set of patterns which you want the perceptron to learn, might be something like the XOR problem. Then no perceptron can be made to recognize your taste. However, there may be some other kind of neural network which can.
If a set of patterns can be correctly classified by some perceptron, then such a set of patterns is said to be linearly separable. The term "linear" is used because the perceptron is a linear device. The net input is a linear function of the individual inputs and the output is a linear function of the net input. Linear means that there is no square(x2 ) or cube(x3), etc. terms in the formulas.
A pattern (x1,x2, ..., xn) is a point in an n-dimensional space. (Stop imagining things.) This is an extension of the idea that (x,y) is a point in 2-dimensions and (x,y,z) is a point in 3 dimensions. The utility of such a wierd notion of an n-dimensional space is that there are many concepts which are independant of dimension. Such concepts carry over to higher dimensions even though we can think only of their 2 or 3-dimensional counterparts. For example, if the distance to a point (x,y) in 2 dimensions is r, then
r2 = x2 + y2
Since the distance to a point (x,y,z) in 3 dimensions is also defined similarly, it is natural to define the distance to a point (x1,x2, ..., xn) in n dimensions as
r2 = x12 + x22 + ... + xn2
r is called as the norm (actually euclidean norm) of the point (x1,x2, ..., xn).
Similarly, a straight line in 2D is given by -
ax + by = c
In 3D, a plane is given by -
ax + by + cz = d
When we generalize this, we get an object called as a hyperplane -
w1x1 + w2x2 + ... + wnxn = T
Notice something familiar? This is the net input to a perceptron. All points (patterns) for which the net input is greater than T belong to one class (they give the same output). All the other points belong to the other class.
We now have a lovely geometrical interpretation of the perceptron. A perceptron with weights w1,w2, ..., wn and threshold T can be represented by the above hyperplane. All points on one side of the hyperplane belong to one class. The hyperplane (perceptron) divides the set of all points (patterns) into 2 classes.
Now we can see why the XOR problem cannot have a solution. Here there are 2 inputs. Hence there are 2 dimensions (luckily). The points that we want to classify are (0,0), (1,1) - in one class and (0,1), (1,0) in the other class.
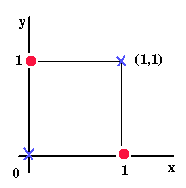
Clearly we cannot classify the points (crosses on one side, circles on other) using a straight line. Hence no perceptron exists which can solve the XOR problem.
During the training period, a series of inputs are presented to the perceptron - each of the form (x1,x2, ..., xn). For each such input, there is a desired output - either 0 or 1. The actual output is determined by the net input which is w1 x1 + w2 x2 + ... + wn xn. If the net input is less than threshold then the output is 0, otherwise output is 1. If the perceptron gives a wrong (undesirable) output, then one of two things could have happened -
In such a case we should decrease the weights. But by how much? The perceptron learning algorithm says that the decrease in weight of an edge should be directly proportional to the input through that edge. So,
new weight of an edge i = old weight - cxi
There are several algorithms depending on what c is. For now, think that it is a constant.
The idea here is that if the input through some edge was very high, then that edge must have contributed to most of the error. So we reduce the weight of that edge more (i.e. proportional to the input along that edge).
Now we should increase the weights. Using the same intuition, the increase in weight of an edge should be proportional to the input through that edge. So,
new weight of an edge i = old weight + cxi
What about c? If c is actually a constant, then the algorithm is called as the "fixed increment rule". Note that in this case, the perceptron may not correct its mistake immediately. That is, when we change the weights because of a mistake, the new weights don't guarantee that the same mistake will not be repeated. This could happen if c is very small. However, by repeated application of the same input, the weights will change slowly each time, until that mistake is avoided.
We could also choose c in such a way that it will certainly avoid the most recent mistake, next time it is presented the same input. This is called as the "absolute correction rule". The problem with this approach is that by learning one input, it might "forget" a previously learnt input. For example, if one input leads to an increase in some weight and an other input decreases it, then such a problem may arise.
Comments/suggestions? Contact: vikram AT iiit.ac.in