Research on Robust and Scalable Solvers for Large Scale Bundle Adjustment and SLAM
Introduction
In this project, we want to explore scalable linear and non-linear solvers for the non-linear optimization problem for bundle adjustment. This problems stems from 3D reconstruction where a 3D shape is reconstructed from images taken by several cameras. So far we have investigated three types of solvers based on preconditioned gradient descent. See below for more details on our work.
Two-Grid Preconditioned Solver for Bundle Adjustment
Authors: Siddhant Katyan, Shrutimoy Das, Pawan Kumar, Winter Conference in Applied Computer Vision (WACV) 2020
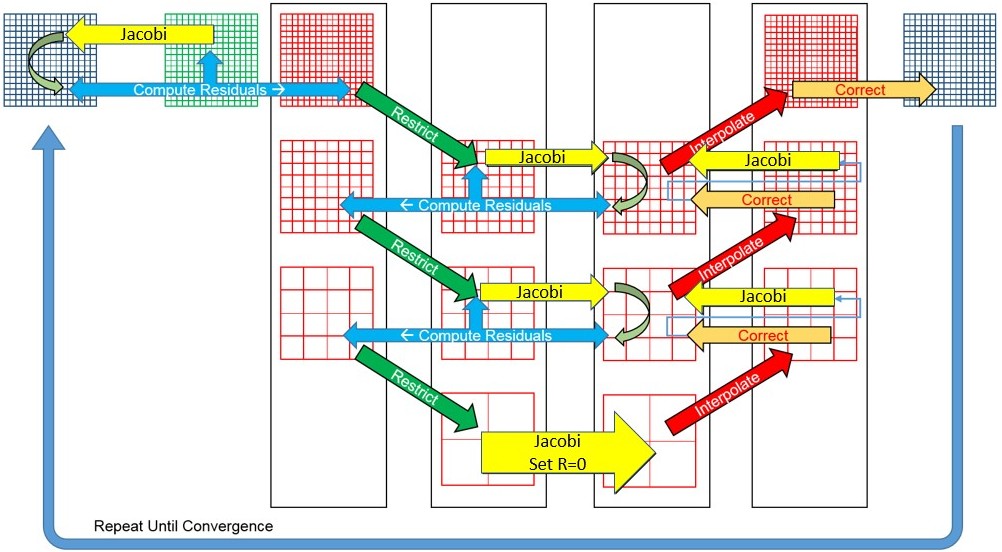
Abstract: Problems for bundle adjustment tend to be very ill-conditioned, the condition number is of the order of roughly 10^20. This creates challenges for the solver, as a result, often diagonal is appended by a perturbation, however, more perturbation may lead to a different problem. One of the most popular solvers in scientific computing for solving PDE based simulations are so-called multigrid methods. In these methods, multiple grids are used to resolve, or damp the error components. However, multigrid methods require certain propoerties of the matrices such as M-matrix property or diagonal dominance. Unfortunately, none of these is satisfied for bundle adjustment problem. In our quest to find a solver on similar principles, we have explored a two-grid like solver.
Inspired from Multigrid, we present the design and implementation of Two-Grid preconditioned Bundle Adjustment (TPBA), a robust and efficient technique for solving the non-linear least squares problem that arises in bundle adjustment. Bundle adjustment (BA) methods for multi-view reconstruction formulates the BA problem as a non-linear least squares problem, which is solved by some variant of the traditional Levenberg-Marquardt (LM) algorithm. Most of the computation in LM goes into repeatedly solving the normal equations that ariseas a result of linearizing the objective function. To solve these system of equations, we use the Generalized Minimal Residual (GMRES) method, which is preconditioned using a deflated algebraic two-grid method. To the best of our knowledge this is the first time that a deflated algebraic two-grid preconditioner has been used along with GMRES, for solving a problem in the computer vision domain. We show that the proposed method is several times faster than the direct method and block Jacobi preconditioned GMRES.
Resources: Sample Matlab Code (full C-code will be uploaded soon), SSBA, PaperA Deflation Based Fast and Robust Preconditioner for Bundle Adjustment
Authors: Shrutimoy Das, Siddhant Katyan, Pawan Kumar, Winter Conference in Applied Computer Vision (WACV) 2021
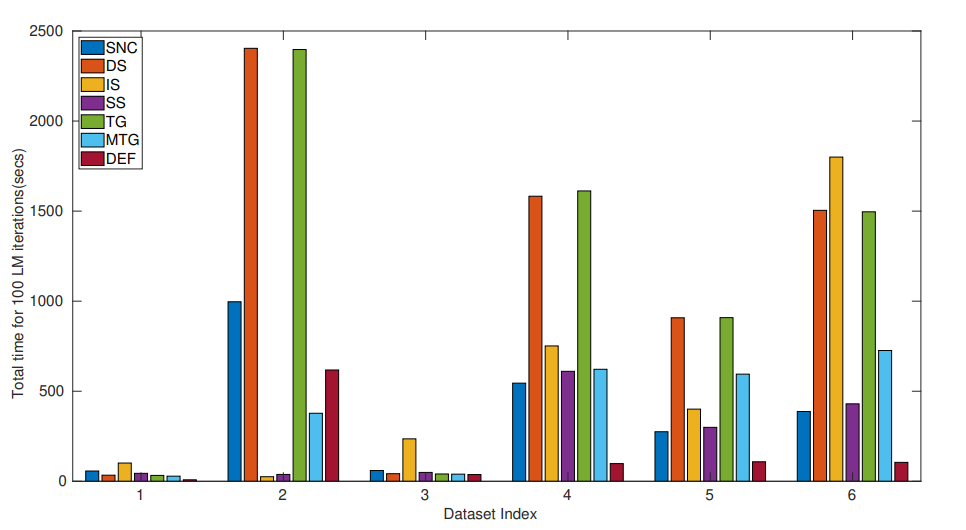
Abstract:
The bundle adjustment(BA) problem is formulated as a non linear least squares problem, which requires the solution of a linear system. For solving this system, we present the design and implementation of a fast preconditioned solver. The proposed preconditioner is based on the deflation of the largest eigenvalues of the Hessian. We also derive an estimate of the condition number of the preconditioned system. Numerical experiments on problems from the BAL dataset suggest that our solver is the fastest, sometimes, by a factor of five, when compared to the current state-of-the-art solvers for bundle adjustment.
Resources: Sample Matlab Code (full C-code will be uploaded soon), SSBA, Paper